Oorspronkelijk gepubliceerd in 2004
Lange vermenigvuldigingen uit het hoofd
Hoeveel is 68355 * 47619?
Het antwoord is: 3 254 996 745, jazeker, maar hoe kom je daar aan zonder rekenmachine? De oplossing ligt erin om de bewerking te verdelen over een hele reeks simpele bewerkingen -bewerkingen die je aankan. Gemakkelijk is het niet. Doenbaar wel.
Een doenbaar voorbeeld
Stel dat iemand jou vraagt hoeveel 132 * 465 is. ('t Is al goed, het is maar hypothetisch.) Je hebt geen papier, geen potlood en geen rekenmachine bij de hand maar je zou die mens toch willen helpen, al is het maar om indruk te maken. Je zou met andere woorden zonder verpinken willen zeggen dat het 61380 is.
Welnu, dat kan je niet. Althans, ik niet. Maar met een beetje respijt kan je het wel, als volgt.
Je zet de twee getallen onder mekaar, in je hoofd of (toegegeven: veel gemakkelijker) op papier. Vervolgens voer je vijf reeksen bewerkingen uit (zie de tekening hieronder). Van de vijf uitkomsten onthoud je telkens het laatste cijfer want dat zijn onderdeeltjes van het woord "eenenzestigduizenddriehonderdtachtig" dat zo meteen over je lippen moet komen.
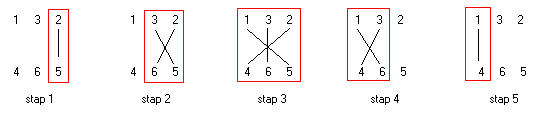
Afbeelding 1: Stappen in de vermenigvuldiging
De eerste bewerking (stap 1 in het schema hierboven) is de simpelste: vermenigvuldig de laatste cijfers van beide getallen, da's 2*5 = 10. Onthoud 0 als "het laatste cijfer van de uitkomst" en draag die 1 over naar de volgende stap.
Voor die tweede stap schuif je 1 cijfer op naar links, je gaat werken met de cijfers 3 en 2 in het eerste getal en 6 en 5 in het tweede. Je vermengvuldigt kruiselings (het meest linkse cijfer bovenaan met het meest rechtse onderaan, en je schuift verder op terwijl je de uitkomsten optelt), dus (3*5) + (2*6). Samen met die overgedragen 1 van daarnet is dat 28, dus onthoud 8 als cijfer en draag de 2 over.
Voor de derde reeks schuif je weer 1 cijfer op naar links, en daarmee komen alle cijfers in beeld. Je vermenigvuldigt kruiselings, in dit geval dus: (1*5) + (3*6) + (2*4) = 31. Plus natuurlijk die overgedragen 2, da's samen 33. Draag die eerste 3 over.
Het ergste is nu voorbij. Je schuift weer eentje op en je vermenigvuldigt kruiselings, dat is (1*6) + (4*3) = 18 plus die 3 van daarnet, dus 21. Noteer de 1 in je hoofd en draag de 2 over.
Nu blijft alleen nog (1*4) over, plus die overgedragen 2, dat is dus 6. Voila, je hebt het. Je roept "61380!" en je kameraden kijken verbaasd op, wat bezielt hem? Leg hen uit dat het de uitkomst is van die berekening van even voordien; het heeft wat tijd gekost omdat je gedronken hebt. Met wat geluk weten ze zelf de exacte cijfers niet meer, dus dan zeg je als uitkomst wat je maar wil, je moet dat zelf aanvoelen.
Besluit
Nadeel van de methode is dus dat je eerst het laatste cijfer van de uitkomst kent en pas helemaal op het laatste het eerste cijfer. Het ware beter omgekeerd. Anderzijds moet je eigenlijk geen tussentijdse resultaten onthouden behalve de cijfers van de uitkomst zelf. je kunt deze methode gebruiken voor getallen van eender welke lengte. Men geeft jou bijvoorbeeld 2 getallen van 10 cijfers. Je schrijft ze onder mekaar, je zet je eraan en zie, enkele minuten later staat de uitkomst er netjes onder, zonder ook maar 1 enkele tussentijdse bewerking. Dat op zich is al straf.
Nee, echt snel gaat het niet, maar met enige oefening is het best te doen.
