Oorspronkelijk gepubliceerd in juni 2024
Hoe ver ligt de horizon?
't Is vakantie en je ligt met een blikje bier in je strandstoel te genieten van een royale plek schaduw. Aan de einder drijft een schip en de vraag komt in je op: "Hoe ver ligt de horizon eigenlijk?".
Ach was dat schip maar nooit voorbijgekomen! Maar gelukkig: een goede wifiverbinding doet wonderen. "Voor een waarnemer op de grond (ooghoogte 1,75 m)", zegt Google, "is op aarde (r = 6371 km) de afstand tot de horizon 4,7 km.". Een kleine 5 kilometer. Voilą, niemand kan nu nog zeggen dat je vandaag niks hebt gedaan. Maar een volgende vraag dient zich aan: hoe berekenen "ze" zoiets?
Een van mijn wiskundeleraren op de middelbare school zei dat wij van alle leerstof die wij kregen, eigenlijk maar twee dingen moesten onthouden. Een ervan ben ik vergeten maar de andere was de stelling van Pythagoras. Met deze stelling los je problemen zoals deze op vanuit je strandstoel. Zonder Google bedoelen we. Het enige dat je nodig hebt, buiten de stelling zelf, is de omtrek van de aarde. Die bedraagt 40000km en als het waar is dat de omtrek van een cirkel gelijk is aan 2πr, dan is de straal van de aardschijf 6369km. (Google maakt er 6371km van, dus we doen verder met 6371).
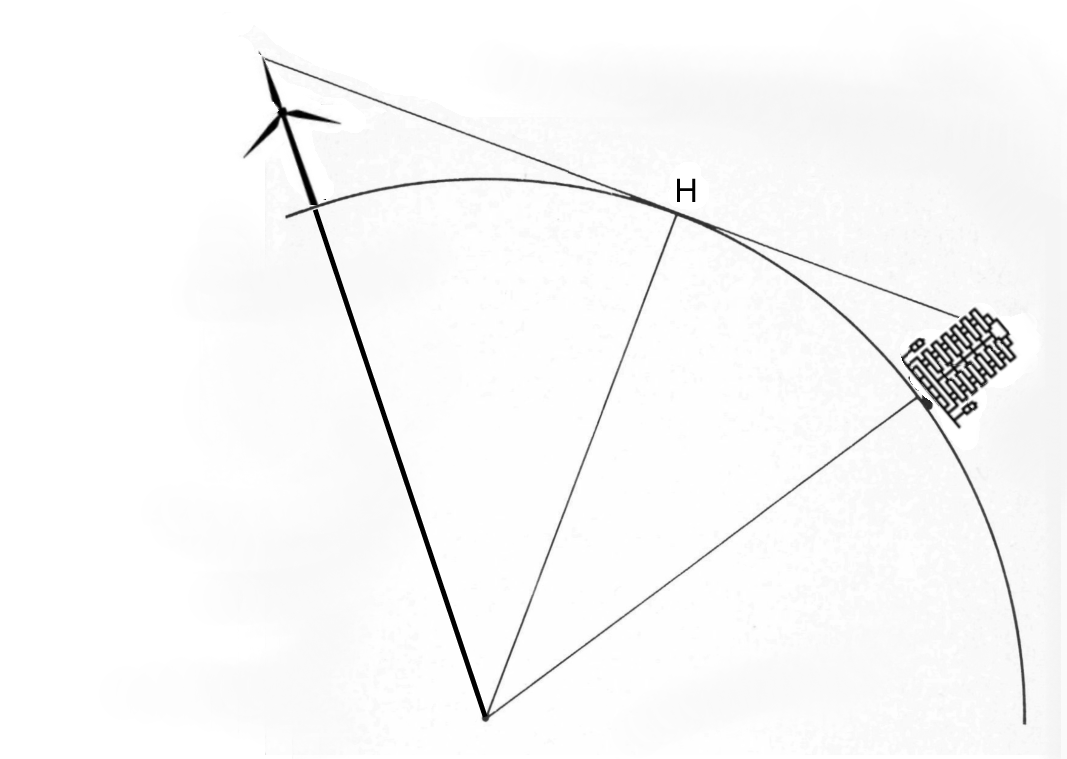
Wat heeft de horizon met driehoeken te maken? Onderstaande tekening, uit Pyth28-5.pdf, juli 1989, maakt het duidelijk:
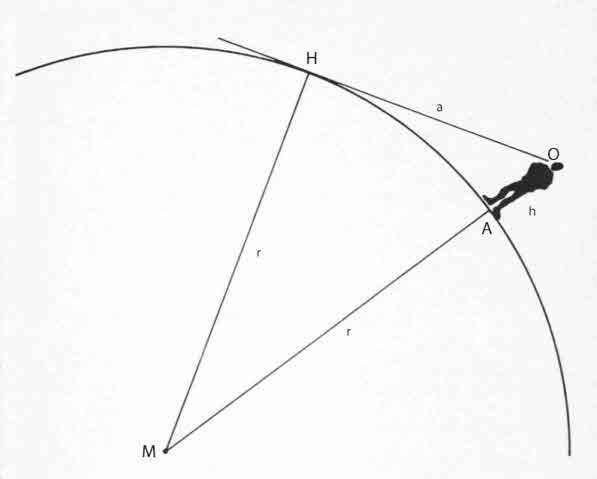
Afbeelding 1: Hoe ver ligt de horizon?
Die kerel op de tekening, dat ben jij. Je bent opgestaan uit je strandstoel ter hoogte van punt A. Je ooghoogte is h (iets minder dan je lengte). De afstand tot H (de horizon) is a. De lijn OH is een raaklijn.
Driehoek HOM is een rechthoekige driehoek. We kennen de lengte van twee zijden ervan: de ene is r, de straal van de aarde, en de tweede is r+h, diezelfde straal met een mens erbovenop. Daardoor is de lengte van de derde zijde te berekenen met de stelling van Pythagoras, want het kwadraat van de schuine zijde (r+h) is gelijk aan de som van de kwadraten van de twee andere zijden (r en a). In dit geval:
- (r + h)2 = r2 + a2
Afstand a, de afstand tussen onszelf en de horizon, is dan te berekenen als volgt:
- a2 = (r + h)2 - r2
- a = √ ((r + h)2 - r2)
- a = √ (2rh + h2) (Formule 1)
We rekenen in meter, dus de straal van de aarde geven we in als 6371000m. De ogen van de gemiddelde mens situeren zich ongeveer 1.60m boven de grond. Samen geeft dit:
- a = √ (2*6371000*1.60 + 1.602)
- a = 4515.2m
De horizon bevindt zich op 4 515m, of 4.5km. Iets minder dan bij Google, maar dat komt omdat ze daar werken met ooghoogte = 1.75m. Hoe groter je bent, hoe verder je kan zien.
Sta je op een ander hemellichaam, dan wordt de uitkomst anders. Op de maan bijvoorbeeld (r=1737.5 km, vraag het aan Google) ligt de horizon volgens Formule 1 op 2358m, zowat de helft van de afstand op aarde.
Een vuistregel
De ooghoogte (h) is sowieso heel klein in vergelijking met r (de straal van de aarde). De tweede term (h2) draagt dus beperkt bij tot de uitkomst. We kunnen de formule vereenvoudigen door dit gedeelte weg te laten:
- a = √ (2rh
Ja, zo zijn we. En als we daarenboven "twee keer de straal van de aarde" (2r = 2 * 6371km) afronden naar "13000000m" (vast!) dan wordt de formule:
- a = √(13000000*h) = 1000* √(13*h)
Met h nog steeds gelijk aan 1.60m, wordt de uitkomst van deze vereenvoudigde formule in ons voorbeeld:
- a = 1000 * √ (13*1.6) = 4560m
Bijna hetzelfde dus als de precieze berekening, zoals het een vuistregel past. Het wordt zelfs nog gemakkelijker als de uitkomst wordt uitgedrukt in kilometer:
- a = √(13*h) (Formule 2)
Deze vereenvoudigde formule geeft de afstand a tot aan de horizon weer in kilometer maar let op, ooghoogte h wordt nog steeds ingevoerd in meter. (Dit vereenvoudigt het rekenwerk en het is niet tegen de natuur.)
Van hoe ver zie je de toren van de kerk?
Stel dat je bent gaan zwemmen en je ben gevaarlijk ver afgedreven van de kust. Tot hoe ver kan je de kerktoren zien van het kuststadje waar je die ochtend je laatste croissant hebt gegeten?
Antwoord: stel dat de toren 50m hoog is (h = 50m). Op het moment dat je nog net het stipje van de toren kan zien, weet je volgens Formule 2 dat het je allerlaatste croissant is geweest, want je bent niet minder dan √(13*50) = 25.5km afgedreven van de kust.
Hoe ver zijn windmolens zichtbaar vanuit je appartement op de dijk?
We blijven aan zee. De burgemeesters van de kuststeden maken zich zorgen over windparken in de Noordzee. Ze vrezen voor visuele vervuiling van de horizon. Wat is daar van aan? Ik baseer mij op een artikel in nr. 53 van het tijdschrift "De Grote Rede", uitgegeven door het Flanders Marine Institute -maar zie mijn bedenkingen verderop.