 Dreticus
Dreticus
Oorspronkelijk gepubliceerd in 2016
Scherptediepte
Inleiding
Scherptediepte hangt grotendeels af van het gebruikte diafragma.
De onderstaande foto's, genomen met een 50mm lens, tonen het verschil in scherptediepte tussen een beeld gemaakt met diafragma f/1.4 en een met f/22.
Een diafragma dat wijd openstaat (zoals f/1.4 of f/2.0), levert een geringe scherptediepte op: de scherpte voor en achter het scherpstelpunt neemt snel af. Een klein diafragma daarentegen (f/22, f/32, ...) zorgt er voor dat een groter gedeelte van het beeld aanvaardbaar scherp is.
Waarom zou iemand opzettelijk een foto nemen die voor het merendeel onscherp is? Meestal is dit om artistieke redenen: een onscherpe voor- of achtergrond kan irrelevante details in het beeld maskeren en kan ook op zichzelf heel mooi zijn.
Een maat voor scherpte
Naar verluidt kan het menselijk oog, vanop een afstand van 25cm, details onderscheiden in een 20x30cm afdruk (we vertalen Amerikaanse meeteenheden in dit artikel ruwweg naar ons decimaal stelsel) tot en met 0.25mm.
Deze vaststelling uit de jaren 30 van de twintigste eeuw (cf. Norman Koren) is uitgegroeid tot een conventie: we bestempelen een punt als "scherp" als het niet meer dan 0.25mm bestrijkt (in een gestandaardiseerde setting).
"Circle of Confusion"
Een lens geeft slechts op één welbepaalde afstand een punt weer als een punt, namelijk op de afstand waar je scherpstelt. Een punt dichterbij of verderaf wordt minder scherp weergegeven. Een standaard menselijk oog zal op een kijkafstand van 25cm punten met een doorsnede van meer dan 0.25mm beginnen zien als vlekjes in plaats van punten.
0.25mm op een 20*30cm afdruk komt overeen met 0.03mm op een filmnegatief van 24x36mm. Daardoor beschouwt men 0.03mm dikwijls als grenswaarde voor de "Circle of Confusion" (CoC), in het Nederlands "verstrooiingscirkel" genoemd. Een punt dat dikker is dan 0.03mm op het negatief (of op de full frame sensor van 24x36mm) wordt niet meer gezien als een enkel punt, maar als een vlekje.
Met deze definitie kunnen we een scherptediepteveld (in het Engels: "Depth of Field", dikwijls afgekort tot "DoF") afbakenen: alles binnen dat veld noemen we gemakkelijkheidshalve "scherp" en alles daarbuiten "onscherp". Alsof we iedereen met een inkomen van minder dan 1500 EUR "arm" zouden noemen en de rest "rijk".
Het scherptediepteveld
Afbeelding 2 (hieronder) illustreert hoe de scherpte gradueel afneemt voor en achter het scherpstelpunt. De grafiek geeft de theoretische onscherpte weer wanneer je een 50 en een 90mm lens gebruikt en scherpstelt op een afstand van 5 meter, met diafragma f/2 en f/4 (full frame). Hoe hoger de waarden op de verticale as, hoe meer onscherpte. (Scherpte wordt hier gemeten door de grootte van de "circle of confusion" op elke afstand.)
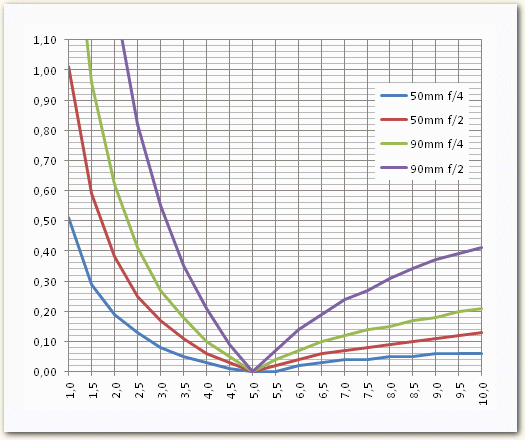
Afbeelding 2: Theoretische onscherpte.
Bijvoorbeeld: wanneer je een 50mm lens bij diafragma f/2 (de rode lijn) scherpstelt op 5,0 meter (zie X-as), dan ) heeft de "Circle of confusion" tussen 2.0 en 2.5 meter (op de X-as) een diameter van 0.30mm (zie Y-as).
We zien dat de scherpte afhangt van het diafragma (f/2 leidt sneller tot onscherpte dan f/4) en van de focale lengte van de lens (een 90mm lens heeft minder scherptediepte dan een 50mm).
De onscherpte is minimaal (0.00 op de verticale as) op 5.0m afstand (horizontale as). Verrassend is dit niet: het is de afstand waarop is scherpgesteld. Het scherptediepteveld van de lens/diafragma-combinatie begint en eindigt waar de lijn door 0.03mm gaat op de Y-as. Het is moeilijk exact te bepalen via de grafiek, maar bij de donkerblauwe lijn is dit van 4.0 tot 6.6 meter. Dit wil zeggen dat met diafragma f/4 en een 50mm lens scherpgesteld op 5 meter, de grenzen van het scherptediepteveld liggen tussen 4.0 en 6.6m.
De onscherpte neemt vooral toe voor het scherpstelpunt. Een punt 1 meter voor het scherpstelpunt wordt even scherp weergegeven als een punt 1.6 meter erachter.
Er zijn vele calculators voorhanden om de grootte van het scherptediepteveld te berekenen. Je kiest vooraf of je met fullframe werkt of met APS-C of nog een ander formaat, want dat bepaalt de "circle of confusion". Vervolgens voer je de focale lengte in van de lens, het gewenste diafragma en de afstand waarop je scherpstelt. Het resultaat zegt dat met die lens en met dat diafragma, en scherpstelling op die afstand, alles aanvaardbaar scherp is van zoveel tot zoveel meter.
Deze uitkomsten uit het hoofd leren voor een reeks focale lengtes en diafragma's is nogal ambitieus. Sommigen geven als vuistregel "de scherptediepte achter het scherpstelpunt is grosso modo 2x groter dan die ervoor" (voor afstanden vanaf 10x de focale lengte van de lens, dus bijvoorbeeld vanaf 0.5m voor een 50mm lens). Dat helpt, zolang je maar beseft dat het zelden klopt (in het voorbeeld hierboven is het bijvoorbeeld 1 versus 1.6 meter). In feite kan je alleen zeggen dat het scherptediepteveld achter het scherpstelpunt minstens even groot is als dat ervoor.
En da's ook al iets. Het helpt als je bijvoorbeeld een foto neemt van een groep mensen die zich in 2 rijen hebben opgesteld, en je weet niet waar precies je best scherpstelt. "Tussen de twee rijen in" lijkt niet slecht maar "op de voorste rij" lijkt toch nog iets beter, want er is meer scherptediepte verderop dan vooraan en die voorste rij komt ook prominenter in beeld. De combinatie van deze overwegingen suggereert scherpstelling op de achterzijde van de eerste rij. Ik zou in praktijk aan iemand uit de achterste rij vragen om ezelsoren te toveren achter het hoofd van iemand uit de eerste rij -gewoonlijk vind je wel een vrijwilliger- en dan daarop scherpstellen. Maar zie dat de vingers niet opnieuw opduiken op het moment van de foto zelf.
Kijk ook eens naar deze DoF simulator, heel interessant. En voor eenvoudige berekeningen is er onze eigenste calculator hieronder. Je krijgt de arbitraire grenzen van het scherptegebied en ook de hyperfocale instelling -waarover we het zodadelijk hebben.
Groothoeklenzen
Men zegt soms dat een groothoeklens meer scherptediepte heeft dan een telelens, maar dat is niet 100% correct. Neem een foto van je model met de twee lenzen -en inderdaad, het beeld van de groothoeklens heeft meer scherptediepte. Maar je model staat ook veel kleiner op de foto. Als je ervoor zorgt dat hij of zij met de twee lenzen evenveel plaats inneemt in het beeld (dit betekent dat hij/zij dichterbij moet komen als je de groothoeklens gebruikt), dan is de scherptediepte vergelijkbaar.
Meer informatie vindt je bv. hier.
DoF calculator (vul waarden in en klik op "Bereken")
Als je experimenteert, zie je dat scherpstellen op een voorwerp dichtbij minder scherptediepte geeft dan scherpstellen op een voorwerp veraf.
Het symbool voor de hyperfocale afstand

Heb je je ooit al afgevraagd wat het symbool met de "bergen" op goedkopere camera's precies wilt zeggen?
Het stelt niet scherp op verafgelegen bergen. Het stelt scherp op de hyperfocale afstand (waardoor alles voldoende scherp wordt tot aan de horizon en niet verder).
Een voorbeeld (f/5.6, APS-C camera): in een weids landschap kan je met een 28mm lens scherpstellen op oneindig. Dan is alles vanaf 7m tot oneindig aanvaardbaar scherp. Maar je kan ook scherpstellen op de hyperfocale afstand (dit is in dit geval 7m, reken maar uit). Dan is alles aanvaardbaar scherp vanaf 3.5m tot oneindig. Da's pas vooruitgang! In het eerste geval is de verte het aller-allerscherpste in de foto; in het tweede geval de voorwerpen op 7m ... en misschien is daar wel niets te zien?
Maximaliseren van het scherptediepteveld: de hyperfocale afstand
Als je uitkijkt over weiden en bossen, op welk punt ga je scherpstellen? Op de horizon? Dan valt het gros van het scherpteveld daar achter, in niemandsland. Op een voorwerp vlakbij? Dan dreigt de achtergrond onscherp te worden.
Om het probleem te minimaliseren, kan je scherpstellen op de hyperfocale afstand. D.w.z. op het punt dat per definitie het meest uitgestrekte scherptediepteveld oplevert, vooraan en achteraan samengeteld. Wij leggen dadelijk uit hoe je dit kan berekenen, maar om de uitleg goed te begrijpen moet je het volgende voor ogen houden. Als je scherpstelt op een punt 10 meter van je vandaan, en je regelt het diafragma zo dat het oneindige nog net binnen het scherpteveld valt (kijk hiervoor naar de markering op je lens), dan zal alles "acceptabel scherp" zijn vanaf de helft van die 10 meter tot oneindig. Stel je scherp op 100 meter, en je regelt het diafragma zo dat het oneindige nog net binnen het scherptebereik ligt, dan is alles acceptabel scherp vanaf 50 meter tot oneindig. Enzovoort enzovoort. Dat is de hyperfocale afstand bij het gekozen diafragma.
Hoe vind je de hyperfocale afstand in praktijk?
Methode 1 is de gemakkelijkste: voer de nodige gegevens in in een DOF calculator, zoals die hierboven.
Methode 2 is iets avontuurlijker. (Gebruik de 50mm lens in Afb. 3 hieronder als visuele hulp):

Afbeelding 3: "Oneindig" uitgelijnd op f/8 (vlak boven de 'T' van PENTAX).
- (1) kies het gewenste diafragma -we nemen als voorbeeld f/8
- (2) lijn het "oneindig" teken op de lens uit met dat diafragma (draai de scherpstelring totdat de 8 van f/8 (vlak boven de 'T' van PENTAX) net onder "oneindig" staat.
De hyperfocale afstand is dan de afstand in het centrum van de schaal (hier: 10m -in werkelijkheid is het 10.4m), en alles zal scherp zijn binnen de afstand gemarkeerd door f/8 links van de middelste streep en de gespiegelde afstand rechts. Hier: tussen oneindig en... tja... een afstand ergens tussen 10 en 3 meter -je weet dat het de helft is van 10.4m. (Voer de gegevens in in de calculator hierboven en je vindt voor dat getal de waarde 5.2m). Dus: stel scherp op 10.4 meter en alles is scherp vanaf 5.2m tot aan de horizon.
In praktijk zijn de markeringen op jouw lens te weinig gedetailleerd, maar je kan het ook zelf uitrekenen met de rekenmachine. De formule is: het kwadraat van de focale afstand gedeeld door het diafragma maal 0.03 (0.02 voor APS-C). Nog preciezer wordt het als je er nog eens de focale lengte bijtelt, maar dat heeft weinig invloed op het eindresultaat. Bijvoorbeeld met een 50mm lens en diafragma f/22 ligt de hyperfocale afstand op 502mm/(22*0.03) = 37888 mm (of 3838mm met die 50mm er nog eens bij). Dit betekent dus dat, als je met een 50mm lens scherpstelt op een afstand van pakweg 4 meter met een diafragma van f/22, dat dan jouw foto voldoende scherp zal zijn vanaf 2 meter tot aan de horizon.
Het mag dan allemaal erg wetenschappelijk klinken, in praktijk zal je je zelden verlaten op die "hyperfocale afstand" omdat er nog zoveel andere factoren een rol spelen. Bedenk dat bijna niets in het scherptediepteveld optimaal scherp is: de scherpte gaat van "zo scherp als maar zijn kan" (ter hoogte van het scherpstelpunt) naar "nog net acceptabel onder de nodige assumpties". Als de bomen aan de horizon belangrijk zijn (of het meest in het oog springen), dan stel je misschien toch beter gewoon scherp op oneindig, want door scherpstelling op de hyperfocale afstand verlies je aan de horizon al meer dan de helft van de scherpte vergeleken met je focuspunt.
Een variant is de "verdubbel de afstand" methode ("Double the Distance"). Je bepaalt het dichtstbijzijnde punt dat scherp moet zijn (bv. een muurtje, een steen, een bloem). En dan:
- (1) kijk op de lens welke afstand dat is
- (2) stel vervolgens scherp op het dubbele van die afstand
- (3) draai aan de diafragma-ring tot het oneindige nog net binnen het bereik is.
Daarmee is de voorgrond (vanaf het gekozen punt) even scherp als de horizon. Hoe scherp is niet gezegd, want dat wordt mee bepaald door het diafragma dat je kiest. Maar er is vooraan evenveel scherpte te vinden als achteraan.
Zie Why hyperfocal distance charts are wrong.



Afbeelding 1a/b/c: Unsharp Mask
Van het oorspronkelijke beeld (bovenste beeld) wordt een onscherpe versie gegenereerd (midden), en het verschil tussen beide versies resulteert in een nieuw beeld dat gebruikt wordt als masker (onderaan).
Scherpte softwarematig opkrikken
"Unsharp Mask"
Je bent het wellicht al tegengekomen als één van de menu-items in je software-programma en je hebt er misschien al wel eens bij stilgestaan... waarom gebruikt men precies de term "unsharp mask" als men de scherpte wilt verhogen?
De term "unsharp mask" komt voort uit de traditionele donkere kamer, maar wij leggen het uit in de digitale donkere kamer. De digitale "unsharp mask"-procedure verloopt als volgt. Eerst wordt er van de originele afbeelding (foto 1) een onscherpe ("blurred") kopie gemaakt (foto 2). (Hoe onscherp, dat bepaal je zelf met de "radius" schuifregelaar in je software). Dan wordt de onscherpe kopie vergeleken met het origineel. Als een pixel qua helderheid erg veranderd is, dan duidt dit erop dat dit puntje op een overgang tussen twee elementen ligt (de rand van een baksteen, een blad, een lijn in een patroon, ...), anders was de waarde van de pixel niet veranderd door de "blur". Dat is gemakkelijk te begrijpen: beeld je immers in dat je een perfect egaal vlak (zonder reliëf, zonder lijn, zonder patroon, gewoon een egaal vlak) onscherp maakt... het beeld vooraf en nadien zal bijna identiek zijn aan het origineel. Neem je daarentegen een beeld met allemaal fijne ruitjes en je maakt dat een beetje flou, dan zal je wèl een groot verschil zien in de buurt van de lijntjes.
Dank zij die onscherpe versie van jouw oorspronkelijk beeld kan het programma dus bepalen waar de hoeken en kantjes zijn, dingen die het meest invloed hebben op de gepercipieerde scherpte, en het genereert daarop een masker dat die contouren weergeeft (foto 3). En dan gebeurt er het volgende:
- men gaat (in het origineel) de helderheid van de punten op en vlak naast de contouren een beetje aandikken: de lichte pixels worden iets lichter, de donkere donkerder. Daardoor valt de overgang tussen de twee meer op voor het menselijk oog en... lijkt het beeld scherper. De sterkte van dit aandik-effect kan je zelf instellen met de "amount"-slider in jouw programma.
- met de "treshold"-slider ("drempel") duidt je aan welke overgangen in aanmerking komen om extra in de verf gezet te worden. Zet je de drempelwaarde te laag, dan worden niet alleen hoeken en kanten (met een grote overgang van licht naar donker) aangescherpt, maar ook subtiele helderheidsgradaties, wat meestal niet de bedoeling is. Zet je de drempelwaarde hoog, dan laat je een groot deel van jouw beeld ongemoeid en concentreer je je alleen op de echte hoekjes en kantjes.
Het resultaat is een beeld dat er ontegensprekelijk scherper uitziet, maar ... dikwijls worden ook kleine onvolkomenheden in het beeld mee in de verf gezet. Dat is vooral zo voor beelden met relatief veel ruis: ruis is dan moeilijk te onderscheiden van detail.
Advies
Zelf ben ik heel conservatief met aanscherpen. Een beetje extra scherpte, om het verlies bij de digitale ontwikkeling te compenseren, is zeker OK. Maar een afbeelding die al scherp is op zichzelf, wint niks als je ze transformeert tot een vlijmscherp ding dat de ogen uitsteekt; en een beeld dat onscherp is om te beginnen, is niet deftig aan te scherpen. Het Internet staat vol foto's die lelijk onrealistisch scherp zijn. Ooit zal men die afdoen als "begin eenentwintigste eeuw, toen de digitale technieken doordrongen tot het grote publiek" -iets in die aard!
Ik zet "sharpening" bij de ontwikkeling (in LightRoom, Capture One, ...) default op 0.
 Dreticus
Dreticus




